Statistics

An unerring compass guiding towards the truth

🎓 What we know 🎓

How many people for a new experiment

The bigger the effect, the smaller the sample size. Or in other words, if you can easily spot the signal of interest (SOI) amid all the noise, you don’t need a lot of data to be confident in your findings.

The problem is that with EEG signals, the effect size is very small. And a bigger problem is that often the effect size is unknown (as well as the other parameters needed).

That’s where the Fitted Distribution Monte Carlo (FDMC) method comes in [(Guttmann-Flury et al., 2019)].

Recipe for FDMC:

Collect data from a historical dataset with similar characteristics to what you plan to collect, or run a small-scale propspective power analysis
Find the variable(s) that best describe the SOI
Fit this (these) variable(s) to a common distribution and estimate the effect size
Using the appropriate parameters (e.g. mean, standard deviation), simulate as much data as needed to achieve a desired statistical power (usually 0.8, with a significance level of alpha = 0.05.

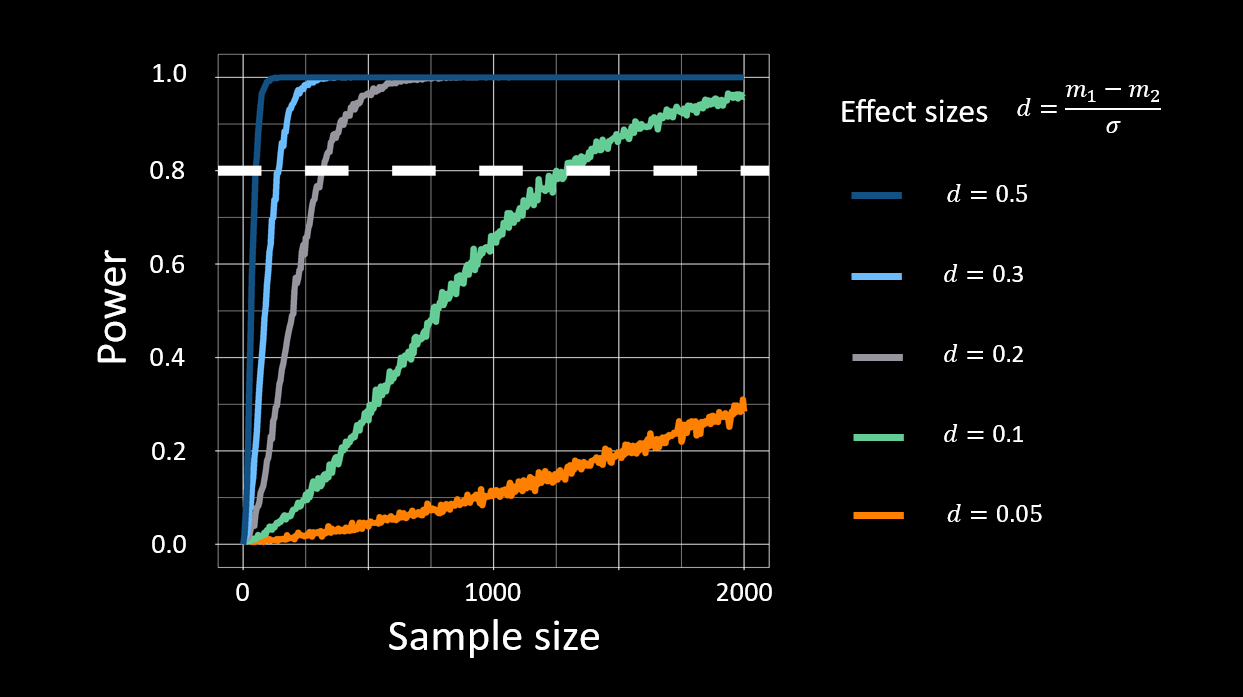
The a priori sample size depends on the estimated effect size. For example, with an effect size of d = 0.1 (in green in the figure below), you’d need around 1250 trials.

Fitted Distribution Monte Carlo (FDMC) Simulation for A Priori Sample Size Estimation

A new visualization tool for confusion matrices: Confusion Ellipses (CE)

So, you’ve estimated your a priori sample size, run your experiment, and gotten some classification results. Now what?

Let’s start by visualizing the results. Confusion matrices (CM) are a great tool for evaluating a classifier’s performance. For a simple two-class problem, the four values in a CM don’t tell you much on their own—but the relationships between them do, revealing insights like class imbalance, accuracy, and other performance metrics.

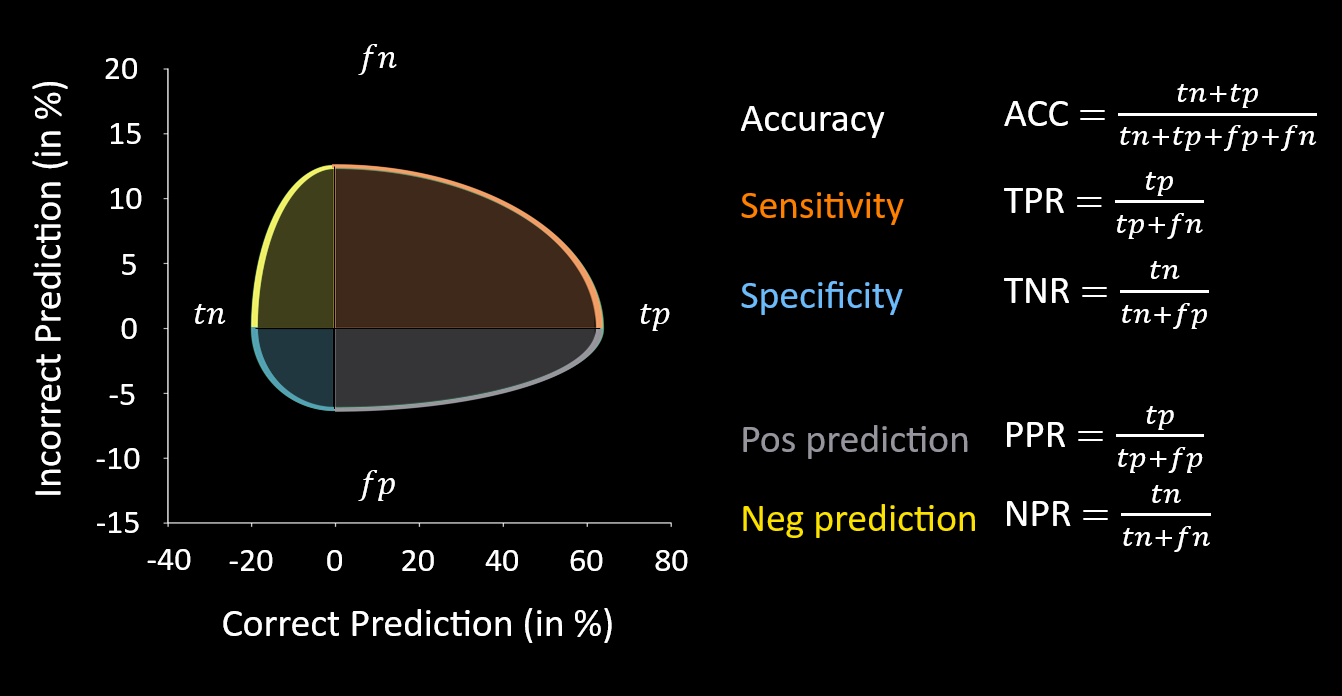
Confusion Ellipse: a new representation of the Confusion Matrix

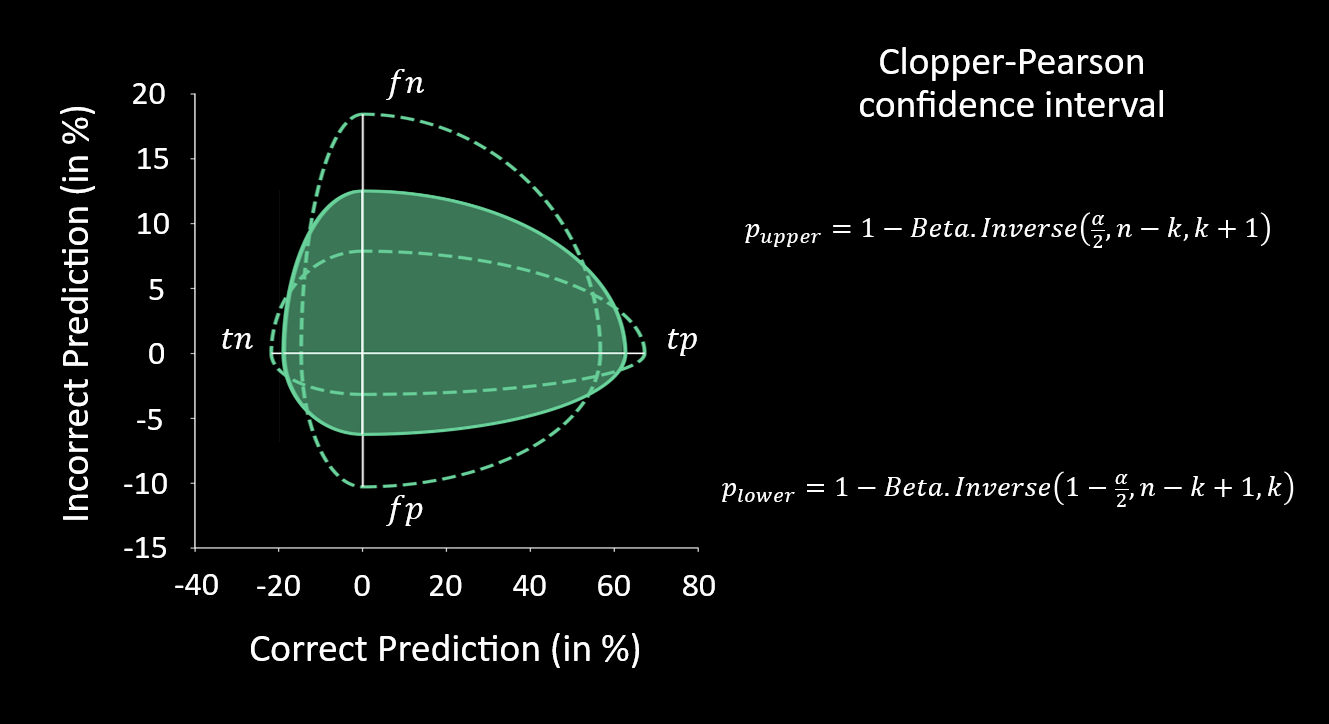
An interesting property of the CM is that it consists of two independent samples, each following a Binomial distribution: True / False (or 0 / 1). And for each distribution, we can estimate the confidence interval (like the Clopper-Pearson interval shown in the figure).

Confusion Ellipse with Confidence Interval

Displaying the confidence intervals on the Confusion Ellipse

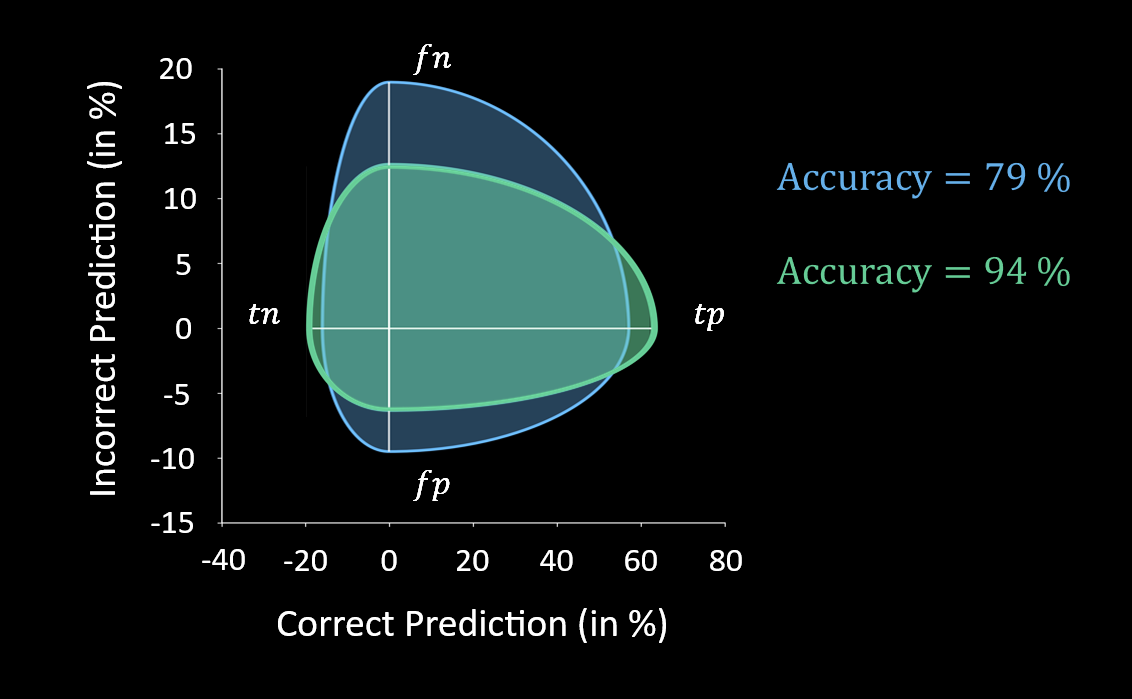
By design, Confusion Ellipses make it easy to compare classifiers at a glance. If a CE is narrower on the horizontal axis (green in the next figure), it indicates a higher accuracy compared to a wider ellipse (blue).

Comparison of two Confusion Ellipses

How much data to prove pipeline A is better than pipeline B

When comparing the performance of two (or more) classification algorithms, the key question becomes: do you have enough data to confidently say that one algorithm performs significantly better than another? In other words, what’s the minimum number of trials needed so that, in 95% of cases (with alpha = 0.05), the confidence intervals for each result do not overlap?

This is where the Distance Separation (DS) method comes in [(Guttmann-Flury, 2023)]. DS measures the level of separation between the confidence intervals at each sample size. The ratio is negative when the required sample size isn’t reached, zero at the critical sample size, and becomes positive thereafter.

Making sure that there is enough data to have a significant difference between two classifiers

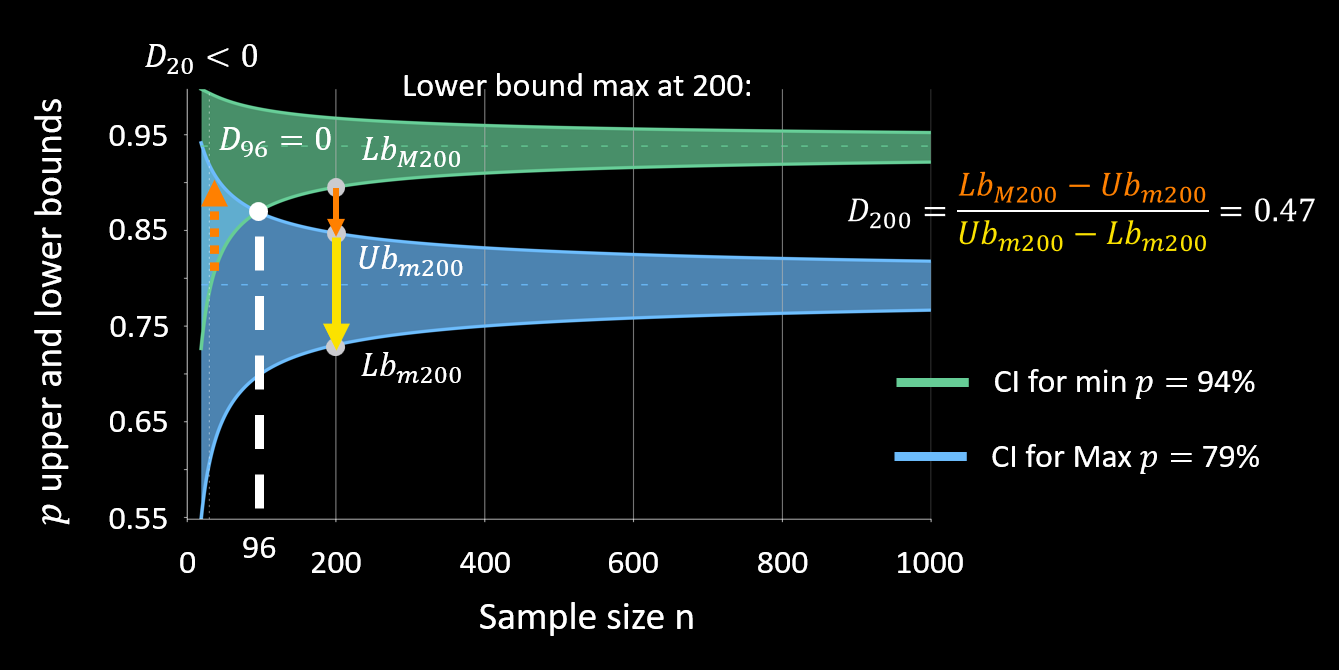
For instance, a green classifier with a 94% accuracy would be statistically significantly better than a blue classifier with 79% accuracy if the results are based on at least 96 trials.

When the difference in classification accuracy between two algorithms is smaller, you’ll need much more data to reach a conclusion.

🤔 What we don’t know (yet) 🤔

What is an acceptable minimum classification accuracy?

Well of course, the higher the better.

However, the acceptable accuracy level depends on the application and the risks involved. For instance, if a BCI controls a car and has a 10% chance of causing a fatal accident, very few would be willing to take that risk. On the other hand, if a BCI offers a 60% chance of improving rehabilitation, many patients might find it worthwhile, even if the improvement is modest.

References

Conference Articles

2019

EMBC 2019
A Priori Sample Size Determination for the Number of Subjects in an EEG Experiment

E. Guttmann-Flury, X. Sheng, D. Zhang, and X. Zhu

In 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Nov 2019

Abs Bib HTML PDF

This paper represents a first attempt to perform a priori sample size determination from a "historic" Electroencephalography (EEG) dataset. The importance of adequate sample size is firstly highlighted, and evidence is given against the use of normal distribution for such computations, when the data cannot be assumed to be Gaussian. The "historic" dataset is then thoroughly examined to determine the least less likely underlying distribution for the desired phenomenon, in this case the spontaneous blinks potential. Two Monte Carlo simulations, using different distribution assumptions, are subsequently computed to estimate the a priori minimum sample size. Finally, these choices are discussed considering practical limitations, as well as the computational differences for other phenomena to study.
@inproceedings{guttmannflury2019apss, title = {A Priori Sample Size Determination for the Number of Subjects in an EEG Experiment}, author = {Guttmann-Flury, E. and Sheng, X. and Zhang, D. and Zhu, X.}, booktitle = {2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC)}, pages = {5180-5183}, year = {2019}, organization = {IEEE}, doi = {10.1109/EMBC.2019.8857482}, url = {https://ieeexplore.ieee.org/abstract/document/8857482}, keywords = {Electroencephalography, Gaussian distribution, Monte Carlo methods, Brain modeling, Computational modeling, Visualization}, }

Theses

2023

SJTU
Innovative artefact elimination and source localization-based feature extraction for EEG BCI pipelines

E. Guttmann-Flury

Shanghai Jiao Tong University, Nov 2023

Abs Bib PDF

In the thriving realm of neuroscience, Brain-Computer Interfaces (BCI) have emerged as a groundbreaking technology that facilitates direct communication between the human brain and external devices or applications. By harnessing the power of neural signals, BCI have the potential to revolutionize various domains, including healthcare, assistive technology, and human-computer interaction. Multiple recording modalities are available for capturing brain activity. Among them, electroencephalography (EEG) devices stand out as a wearable, comfortable, and cost-effective solution that provides high temporal resolution to non-invasively monitor basic user intentions.

This research is dedicated to the rigorous investigation of motor imagery, with a specific focus on discerning patterns associated with grasping movements of the right and left hands. The ultimate objective is to achieve the highest possible classification accuracy of user intent without the need for neurofeedback or additional indirect information. The limitations of EEG in terms of signal-to-noise ratio and spatial resolution necessitate the use of source localization techniques, which can unveil the intricate dynamic interactions and connections within the brain. To easily distinguish between existing algorithms and the new ones introduced in this research, the original acronyms and appellations will be noted in bold.

Ensuring the accuracy and reliability of EEG data analysis requires the homogeneity of electrode functioning and the cleanliness of signals in the vast majority of cases. This entails addressing two primary objectives: eliminating statistically significant (and consequential) artifacts and rectifying any malfunctioning electrodes. The spontaneous blink represents a major physiological disturbance, occurring simultaneously with the neural signal of interest with an average probability of 10%.

These considerations led to the design of a multi-modal dataset targeted at comprehensively recording every aspect of the blinks using EEG, electrooculography, electromyography, eye tracker, and high-speed camera. Additional paradigms, including motor execution, P300, and steady-state visual evoked potentials have also been investigated due to their relevance in inferring a comprehensive understanding of the underlying neural mechanisms during MI.

The Fitted Distribution Monte Carlo (FDMC) simulation is first conducted for a priori sample size estimation during a prospective power analysis. The goal is to ensure that sufficient data will be collected to truly comprehend the intricacies of the cortical phenomenon. FDMC demonstrates its superiority by lowering the sample size requirement by 35% compared to the Normal distribution (and by seven times compared to traditional power tables). FDMC is of particular interest when only limited resources or time are available.

The resulting multi-modal dataset facilitated the development of a robust model for accurately classifying and correcting blink artifacts as well as removing bad channels from the EEG data. The Adaptive Blink Correction and De-drifting (ABCD) algorithm has proved to improve the overall data quality and displays significantly better results than the state-of-the-art, i.e., Independent Component Analysis (ICA), or Artifact Subspace Reconstruction (ASR). The classification accuracy, along with its confidence interval at 95% confidence level, reveals a mean classification accuracy of 93.81% [74.81%; 98.76%] for ABCD against 79.29% [57.41%; 92.89%] for ICA or 84.05% [62.88%; 95.31%] for ASR.

A combination of various innovative algorithms is implemented to extract the most prominent signal of interest (SOI) across the temporal, spatial, and frequential domains. Source localization is first computed on the ABCDcleaned EEG data. The Source Localized Spatio-Temporal (SLST) features approach is applied to capture the spatio-temporal characteristics of the SOI by analyzing the similarities across multiple trials. To further enhance the classification process, a Dual Classifier (DC) is implemented, utilizing both the spatial locations and time-derived covariance matrices from the SLST feature extraction algorithm. The class-specific Fréchet means, along with all other covariance matrices, are computed at the Core Channel Selection, which is determined based on a comprehensive meta-analysis.

Comparisons across different frequency bands (delta, theta, alpha, and beta), filter types (Butterworth, Chebyshev, and Elliptic), and re-referencing, e.g., Common Average Reference, Large and Small Laplacian spatial filters, are also carried out to reveal the optimized combination of all these processing steps. To ensure a fair comparison, all data are first pre-processed with ABCD, re-referenced with the Large Laplacian filter and filtered with a beta pass-band Butterworth filter, as this combination of various filters proved to yield the best accuracy.

A new introduced Consistency computation serves to validate classifiers’ stability and can thus be used to confirm the hierarchy between them, revealing that our SLST+DC method yields a mean classification accuracy of 95.03% (SD = 3.41%). The commonly employed Common Spatial Pattern (CSP) coupled with Linear Discriminant Analysis (LDA) yields 89.16% (SD = 1.76%) or 88.99% (SD = 1.60%) when coupled with Support Vector Machine (SVM). Comparisons were also made with newer methods such as the Minimum Distance to Riemannian Mean (MDRM) that achieved 81.13% (SD = 4.64%) and Tangent Space (TS) 86.09% (SD = 4.48%). All the results issued from the various pipelines are then compared using their confusion matrices.

More generally, confusion matrices (CM) consist of two independent samples (positive and negative), each following a Binomial distribution. To extend their utility, the confidence intervals (CI) are calculated for the probabilities associated with each sample. A complementary estimation of the minimum sample size is presented based on the Distance Separation (DS) method relying on the chosen CI approximation. DS can serve as a viable alternative to FDMC for experimental design, specifically aimed at evaluating the statistical distinction between two classifiers possessing known accuracies. Finally, a method to estimate the accuracy though standard deviation of CI (SDCI) is presented and applied to visual representations of CM, called Confusion Ellipses (CE).

Comparisons with PyCM, a Python library dedicated to CM evaluation and comparison, shows that their computations seem to underestimate the CI mean widths around zero compared to SDCI. Various CI approximations are also tested to assess the influence of the CI approximation choice and can serve as reference when designing a new experiment with the goal of comparing two pipelines with known global classification accuracies. The applicability of these novel methodologies (i.e., SDCI, DS, CE) extends far beyond the confines of the BCI field, encompassing a wide range of domains and disciplines.
@phdthesis{guttmannflury2023thesis, title = {Innovative artefact elimination and source localization-based feature extraction for EEG BCI pipelines}, author = {Guttmann-Flury, E.}, school = {Shanghai Jiao Tong University}, year = {2023}, month = nov, keywords = {Brain-Computer Interface (BCI), Electroencephalography (EEG), Spontaneous blinking, Artifact removal, Sample size calculation, Channel selection, Source Localization, eLORETA, Confusion Matrix (CM), Accuracy confidence interval}, }